Ice sheet models

This page is part of the topic Models of the physical and biological environment of the Antarctic

The first numerical modeling involving the entire Antarctic Ice Sheet was the diagnostic study of Budd et al. (1971) aimed at deriving physical characteristics of the ice sheet, in particular the temperature distribution (obtained from a moving-column model) and balance velocities. In the early 1980s, depth-averaged time-dependent models were first applied to simulate evolution of the Antarctic Ice Sheet in the studies of Budd and Smith (1982) and Oerlemans (1982a,b). Subsequently, models have been modified to include calculation of englacial ice temperature, inclusion of ice-shelf flow, and deformation of subglacial sediments. A recent overview of the status of Antarctic models is provided by Huybrechts (2004). For the present discussion, suffice to note that for land-based flow the so-called shallow ice approximation (SIA) is adopted with the local driving stress balanced by drag at the glacier base (Nye, 1957; Hutter, 1983). In that case, the dominant strain rate is vertical shear and an analytical expression for the depth profile of the horizontal velocity can be readily derived (Van der Veen, 1999a, section 5.1). Essentially, this incorporates the same simplified ice dynamics as did the pioneering work of Mahaffy (1976). Thermodynamics are included following Jenssen (1977) with conservation of energy considered at discrete depth layers extending from the ice surface to the bed or including several layers into the bed underneath. Seddik et al. (2008) proposed an application of a continuum-mechanical model for the flow of anisotropic polar ice to the EDML core, Antarctica.

Realistic model simulations of the behaviour of the Antarctica Ice Sheet over time require adequate surface and lower boundary conditions. More than 2000 reports of SMB determinations are available over Antarctica (e.g. Vaughan et al., 1999), and many of these are on the plateau. However, the Antarctic is very big and more measurements are still needed. While some airborne radar sounding has been conducted, resulting maps of basal topography (Drewry, 1983; Lythe et al., 2000) reflect at best the large-scale topography. Localized channels, if existing, are not captured in these compilations but may exert important controls on ice drainage, especially through outlet glaciers. Discussion here focuses on the ice-dynamical component of Antarctic ice-sheet models, and, specifically, on their ability to simulate contemporaneous rapid changes. A more expanded discussion of the shortcomings of existing ice sheet models is provided by Van der Veen and ISMASS (2007).

Over the past two decades or so, evidence for active ice sheets – both in the past and present-day – has mounted and the traditional view of ice masses responding sluggishly to external forcings has been replaced by the understanding that large ice sheets can undergo rapid change. In West Antarctica, ice streams draining into the Ross and Ronne-Filchner ice shelves have been identified and some of these have been the subject of extensive field campaigns aimed at better understanding the controls on ice streams (c.f. Alley and Bindschadler, 2001, for a collection of papers summarizing earlier findings). These ice streams appear to be capable of rapid changes including margin migration and complete shut-down. Based on mapping of grounding-line positions of Pine Island Glacier using satellite radar interferometry, Rignot (1998a) inferred a retreat of 1.2 ± 0.3 km/yr between 1992 and 1996, corresponding to a thinning rate of 3.5 ± 0.9 m/yr for this glacier. Satellite radar altimetry over the period 1992 to 1999 confirmed this inferred thinning rate and also showed thinning to extend far into the interior (Shepherd et al., 2001). Comparison of the satellite altimetry data with airborne laser altimeter surveys showed that thinning rates near the coast during 2002-2003 were significantly larger than those observed during the 1990s and the Amundsen Sea sector of the West Antarctic Ice Sheet appears to be out of balance by as much as 60% (Thomas et al., 2004a). In the Antarctic Peninsula, several of the peripheral ice shelves have disintegrated or retreated, with a total area in excess of 14,000 square kilometers lost over the past two decades. Vaughan et al. (2003) linked ice shelf collapse to southward migration of the -9ºC isotherm, presumed to correspond to the thermal limit of ice shelf viability. While Vaughan (1993) reported no significant acceleration of input glaciers following the breakup of the Wordie Ice Shelf, elsewhere in the Peninsula ice shelf break-up has led to flow acceleration of grounded glaciers (e.g. Rott et al., 2002; De Angelis and Skvarca, 2003; Rignot et al., 2004a). These observations suggest that the West Antarctic Ice Sheet may be on the verge of contributing to future sea level rise, and have reinvigorated the long-standing debate about the stability of this marine-based ice sheet and to what extent buttressing ice shelves control drainage from the interior.

The current generation of whole ice-sheet models cannot reproduce the observed rapid changes, which led James Hansen to conclude that “ice sheet models cannot be used with confidence for assessing expected sea level change until they demonstrate realistic forcing yielding realistic rates of ice sheet demise” (Hansen, 2005, p. 273). From an ice-flow perspective, the most important yet least understood processes to be included in Antarctic models are dynamics of ice streams and the transition to ice shelf spreading, grounding-line migration and stability, and the interaction between ice shelf break-up and discharge from grounded glaciers formerly draining into these shelves. New analytical treatments of the ice stream to ice shelf transition (Schoof, 2007) suggest the way forward, but at present, the best global models have been unable to include the recently observed activity of ice sheets (IPCC, 2007).

Ice streams, embedded in slow-moving ice, are the primary drainage conduits evacuating ice from the interior to peripheral ice shelves and from thereon to the oceans. In West Antarctica, these ice streams rest on a layer of weak and possibly deforming till offering little resistance to ice flow, implying that flow resistance is concentrated at the lateral shear margins and transferred to excess basal drag under the adjacent interstream ridges (Van der Veen et al., 2007). The exact nature of this transfer of stress is not well known but may ultimately determine inward or outward migration (Raymond, 1996; Raymond et al., 2001; Jacobson and Raymond, 1998). Moreover, Van der Veen et al. (2007) estimate that meltwater production under the shear margin adjacent to Whillans Ice Stream is comparable to that under the ice stream itself, suggesting that these margins could be an important source of water for maintaining basal lubrication under the ice stream. These processes are not included in existing continental-scale models whose spatial resolution is usually insufficient to capture an entire ice stream, let alone the much narrower shear margins. Instead, ice streams are usually simulated through enhanced basal sliding where the basal ice reaches the pressure-melting point. Interestingly, a model study on the dynamics of the Siple Coast ice streams based on this concept generated a cyclicity with stagnant and active ice streams, caused by competition between several preferred ice-flow pathways in the area (Payne, 1998). However, this result may be more fortuitous than reflecting the real physical processes, as noted by the author of that study.

Ice streams represent the transition from interior flow to ice shelf spreading. At the inland boundary of the West Antarctic ice streams, smaller tributaries form within well-defined troughs (Joughin et al., 1999) and over sedimentary basins (Anandakrishnan et al., 1998; Bell et al., 1998) that coalesce into major ice streams. As the streams flow outward and enter the ice shelf, the flow regime becomes more akin to ice shelf spreading. Conceptually, ice streams may be viewed as the transition from internal flow dominated by vertical shear, to ice shelf spreading controlled by longitudinal stress gradients and lateral drag. MacAyeal (1989) developed the so-called “shelfy-stream” model to incorporate this transition into a numerical model simulating large-scale flow over a viscous sediment. This approach, or one similar to it, has yet to be incorporated into whole ice sheet models.

Ever since the pioneering work of Mercer (1968, 1978) and Weertman (1974), glaciologists have speculated that removal of peripheral ice shelves and floating ice tongues will result in increased discharge of interior ice. Over the last two decades, ice shelves in the Antarctic Peninsula have disintegrated, probably in response to a local warming trend that caused the thermal limit of ice shelf viability to migrate progressively southward (Vaughan and Doake, 1996; Vaughan et al., 2003). Velocity measurements on grounded glaciers formerly draining into these ice shelves show that a speed-up followed collapse of the ice shelves (De Angelis and Skvarca, 2003). While many in the glaciological community have interpreted these observations as evidence for the instability models proposed by Mercer and Weertman, and many others since, a more careful analysis of the sequence of events is needed to establish unambiguously to what extent forcings at the calving front propagate upstream and influence discharge from the interior. For example, it could be that increased speeds on the grounded portions resulted from the same surface melt event(s) that led to the collapse of the floating part, rather than reflecting the glacier response to loss of ice shelf buttressing. If, indeed, discharge from the interior is affected by ice-marginal processes, an important question is whether ice shelf collapse necessarily leads to irreversible glacier retreat or whether interior flow will adjust to the perturbation by reaching a new equilibrium. Modeling experiments on the response of Pine Island Glacier to perturbations at the grounding line indicate that a new equilibrium is reached after ~150 years following an imposed instantaneous change on the ice plain (Payne et al., 2004).

At present, understanding of the effects of ice shelf weakening or break up on discharge from the interior is insufficient to incorporate into numerical models. To gain better understanding, targeted data collection and hypothesis testing is needed for identifying processes responsible for rapid glacier changes. Fortuitously, perhaps, the southward migration of ice shelf collapse and consequent flow adjustment of grounded ice in the Antarctic Peninsula offers the opportunity to study a range of glacier settings. The importance of observing a range of grounding-line behaviours is evidenced by the study of Vieli and Payne (2005), who compared various model formulations applied to the study of marine ice sheets. They found that predicted grounding-line migration is dominantly controlled by the way grounding line motion is treated in the numerical model (e.g. fixed grid versus a moving grid), and how the governing equations are discretisized. Physics incorporated into the numerical models, such as longitudinal momentum coupling between the ice shelf and the grounded ice sheet, appeared to be of secondary importance only. The implication of this model comparison is that there is an urgent need to develop better models whose predictions are not dictated by numerical specifics. As concluded by Vieli and Payne (2005), “further model development also requires a better observational history of grounding line migration (in terms of both the timing and spatial extent) and also indicates the need of a test data set for the modeling community.”

Rapid ice-sheet changes originate in, and spread from, restricted regions of fast flow such as ice streams and outlet glaciers. Existing models are based on the shallow-ice approximation (SIA) and do not include longitudinal stresses and the buttressing effects of ice shelves that may restrain ice-stream flow in these key regions. The SIA is appropriate only for slow-moving inland ice where resistance to glacier motion is entirely concentrated at the glacier bed. On the other end of the modeling spectrum is the Morland-MacAyeal (MMF) formulation for ice shelf spreading in which basal drag is set to zero and ice flow is assumed to be depth-independent. It seems likely that flow of fast-moving ice streams and outlet glaciers falls somewhere in between these two model regimes. Thus, the best way to model the dynamically important ice streams is to solve the full stress equations without a priori simplifying assumptions. Doing so on a sufficiently fine grid to resolve the ice streams is too computationally intensive for the current generation of computers; a possible solution would be to follow the climate modelers’ lead and develop variable-resolution models, through use of nested mesoscale models embedded in coarse-grid models, or variable-element size models with adaptive regridding if needed.

Traditional models of ice sheets employ a fixed horizontal resolution over the whole domain and so either fail to resolve these features adequately (if they employ a relatively coarse ~20 km resolution), or would require unfeasible computing resources (if they employ a more reasonable ~1 km resolution). A solution to this dilemma is the application of a nested grid in which the whole domain is modeled at a coarse resolution, while areas of supposed importance such as ice streams are modeled at a series of finer resolutions with the remainder of the slow-flowing interior omitted. A wide range of variable resolution techniques are available ranging from simple ones in which the areas to be modeled at finer resolution are predetermined and held fixed, to ones in which the solution algorithm itself determines which areas are to modeled at the finer resolution. Similarly, the way information passes between the various grids can vary in sophistication from the coarse grid providing boundary conditions to the finer grid, to full multi-grid techniques in which information flows both ways in an iterative fashion. This type of approach is well developed in ocean and atmospheric modeling, and a number of software libraries exist to facilitate the use of nested grids.

To place any confidence in model predictions, it is first necessary to demonstrate that the models can successfully reproduce past glacier variations. Consequently, it is imperative that data sets be developed against which the skill of the numerical models can be tested. In this respect, it is important to separate data used for model calibration (i.e. parameter adjustment) from those used to evaluate the model performance. A more extensive discussion of the more philosophical underpinnings of model evaluation can be found in Van der Veen (1999b), while Van der Veen and Payne (2003) discuss a more pragmatic approach.

An Example Model

2.33 Bed elevations of the Amundsen Sea Embayment area: (left) from circa 2001 (BEDMAP) data compilation (Lythe et al., 2001) and (right) from newer circa 2005 airborne geophysical surveys (Holt et al., 2006; Vaughan et al., 2006). Blue is below sea level, with deeper blue signifying greater depths. The Amundsen Sea is in the lower left corner. Comparison shows that the recent surveys provided a more detailed representation of the subglacial topography.

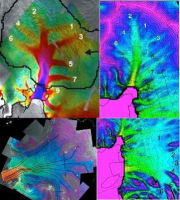
Recent results from the University of Maine Ice Sheet Model (UMISM) are illustrative of current capabilities of the latest generation of ice sheet dynamic models. This example focuses on simulating the ice kinematics of the Amundsen Sea Embayment region (Fastook and Sargent, 2004). Recent airborne geophysical surveys of the region measured new details of the ice thickness and bed elevations (Holt et al., 2006; Vaughan et al., 2006). These data are now available as a 5 km gridded data set in a format convenient for modeling. Figure 2.33 shows the new dataset (right) contrasted with the older BEDMAP dataset (left) for comparison. Gross details are found to be similar, but details within the trunks of the Pine Island Glacier (PIG) and the Thwaites Glacier (TW) allow models to simulate observed flow more accurately (Lang et al., 2004; Rignot et al., 2004b).

The nest of UMISM embedded models begins with a 40 km grid of the entire ice sheet with 16,263 nodes. Embedded in this is a 10 km grid (9000 nodes) that includes the entire Amundsen Sea Embayment measurement area. Nested inside this medium-resolution grid are two 5 km grids encompassing Thwaites and Pine Island Glaciers (6402 and 10,920 nodes, respectively). This procedure produces high-resolution results with very reasonable runtimes. The model reaches the modern position by being run for 40,000 years, from an initial configuration to the Last Glacial Maximum and then from the LGM to the present. The 40,000 year cycle ensures that the final configuration includes time-dependent effects such as transient internal temperatures and isostatic adjustment. It is not sufficient to run the model in steady state for the present configuration and expect the model snapshot to correspond with reality. Model advance and retreat is controlled by a "thinning-at-the-grounding-line" parameter because the internal calculation of grounding line dynamics remains an extremely challenging issue and one that has only recently been solved analytically (as discussed earlier). The grounding line position is determined in this model through spatially non-uniform specification of this parameter, so retreat is guaranteed to halt at the correct position.

2.34 Nested grids, with ice thickness fields, for the UMISM. (A), the full ice sheet at 40 km resolution; (B), a medium resolution, 10 km grid encompassing the whole airborne geophysical dataset (shown in Figure 2.33); full 5 km resolution grids for (C) Pine Island Glacier and (D) Thwaites Glacier. Color elevation scale is shown at right.

2.35 Comparison of model and observed surface velocities for Pine Island Glacier (upper right and left (Rignot et al., 2004b), respectively) and for Thwaites Glacier (lower right and left (Lang et al., 2004), respectively).

Basal conditions are critical and in this case, water is produced, which leads to basal lubrication and higher ice flow rates, when the temperature reaches the pressure melting point. This happens first in the deeper channels and is one reason the dendritic pattern of modeled velocities agrees well with the observed field, however, such a mechanism does not guarantee the excellent agreement between modeled and observed velocity magnitudes (Figure 2.35).

The viscosity of ice is a strong function of temperature, so it is important to include the thermal evolution in predictive models of the ice flow. Retreat of grounding lines to colder, stiffer ice inland could act to stabilise the margin. Measurement of englacial (within-ice) temperatures requires boreholes to be drilled into the ice. This has been possible at a number of sites using hot water drilling (Engelhardt, 2005), but there is still a shortage of information for testing models that couple the ice flow and temperature. Because the presence or absence of water plays such a large role in the dynamics of the ice sheet, the temperature within the ice, and the flux of geothermal heat can have a critical role in determining the rates of ice discharge.